Hattie listed these 3 meta-analyses and effect sizes (ES) as the basis for his average ES = 0.21.
A number of peer reviews highlight that Hattie's interpretation contradicts that of the original studies, e.g., Barwe and Dahlström (2013) ,
"here we have three meta-studies that show a strong connection between class reduction and student achievement, but in Hattie's synthesis this conclusion does not emerge. That's remarkable." (translated from Swedish p. 22)
Hagemeister (2020) also analysed the studies Hattie referenced & details Hattie's many significant mistakes & highly questionable interpretations.
A full copy of Glass & Smith here & contact me for copies of the other 2 studies.
A Detailed Look at the 3 Studies
Glass & Smith explore a range of class sizes reductions & summarise their results in a graph (p. 15).
Hattie in VL says he focused on class size reductions of 25 down to 15 (p. 87). But the study does not report 0.09 for class size of 25 down to 15. It seems Hattie averaged of ALL the DIFFERENT class size reductions!
Hagemeister (2020) also questions Hattie's calculation,
"Hattie gives an effect size of d = 0.09 for Glass and Smith’s study in his Table 6.2. Neither Visible Learning nor his 2005 paper explain how he calculated this value. We might surmise that Hattie summarily synthesised the findings of both ‘well-controlled’ and ‘poorly-controlled studies’. The minimal effect size of d = 0.09 obscures the essential finding by Glass and Smith (1979) that small classes may be successful when their composition is socio-economically balanced." (p. 8)
Glass & Smith (1979) also warn of Hattie's approach,
"over all comparisons available-regardless of the class sizes compared- the results favored the smaller class by about a tenth of a standard deviation in achievement. This finding is not too interesting, however, since it disregards the sizes of the classes being compared." (p. 10).
I also contacted Prof Glass to ensure I interpreted his study correctly, he kindly replied,
Glass & Smith also conclude,
Barwe and Dahlström (2013) also pick-up on this issue and agree that Hattie misrepresents this study by reporting one effect size (p. 16).
"The curve for the well-controlled studies then, is probably the best representation of the class-size and achievement relationship...
A clear and strong relationship between class size and achievement has emerged... There is little doubt, that other things being equal, more is learned in smaller classes." (p. 15).
The Education Endowment Foundation (EEF) also confirm Glass & Smith's finding,
"The evidence suggests that significant effects of reducing class size are not seen until the number of pupils has decreased substantially (to fewer than 20 or even 15 pupils)." Class Size Report July 2021.
Hattie NEVER reports this finding, even though he states it was Gene Glass's invention of the meta-analysis methodology which inspired him to pursue the meta-analysis technique (Lovell, 2018, @9mins).
Also, Glass had warned about Hattie's peculiar method,
"The result of a meta-analysis should never be an average; it should be a graph." (in Robinson, 2004, p. 29)
Bergeron & Rivard (2017) reiterates,
"Hattie computes averages that do not make any sense."Thibault (2017) in "Is John Hattie's Visible Learning so Visible?" also questions Hattie's method of using one average to represent a range of studies (translation to English),
"We are entitled to wonder about the representativeness of such results: by wanting to measure an overall effect for subgroups with various characteristics, this effect does not faithfully represent any of the subgroups that it encompasses!
...by combining all the data as well as the particular context that is associated with each study, we eliminate the specificity of each context, which for many give meaning to the study itself!"
Contrary to Hattie, who consistently claims there is no difference in moderators (age & subjects) Glass & Smith also conclude,
In his 2020 defense, Real Gold Vs Fool's Gold, Hattie responded to the claim that he reports a different conclusion to that of the actual authors of the studies (p. 12),"The class size and achievement relationship seems consistently stronger in the secondary grades than in the elementary grades." (p. 13).
If you look at this meta-analysis in more detail a totally different STORY emerges, which is not represented by Hattie only using one average.
Gene Glass, also wrote a book with 20 other distinguished academics, '50 Myths and Lies That Threaten America's Public Schools: The Real Crisis in Education', which contradicts Hattie,
In Myth #17: Class size doesn't matter; reducing class sizes will not result in more learning, the 21 scholars collaboratively say,
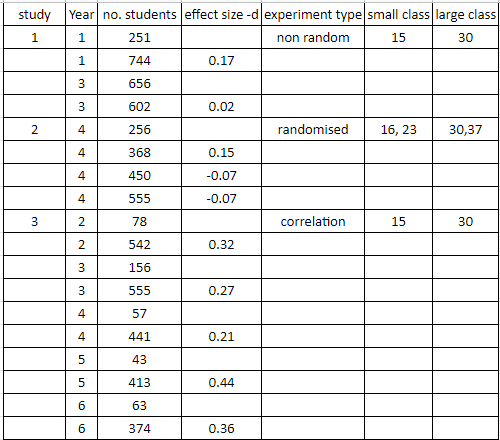
This study was only on 2nd-year students with properly controlled studies using experimental and control groups (although not randomly assigned). They decided a more pragmatic definition of a large class size is about 26 and a small class size is about 19 (p. 49).
So this study is specifically comparing a class size of about 26 students with 19 students.
So this is a totally different study than the Glass & Smith study above, which was looking at a range of different class size comparisons.
Barwe and Dahlström (2013) also point out the difference between this and the Glass & Smith study. Also, they point out Hattie claimed his focus was on reducing 25 students down to 15, which is different to reducing 26 students down to 19 (p. 19).
McGiverin et al., state that, the lack of experimental control and diverse definitions of large and small are among the reasons cited for inconsistent findings regarding class size (p. 49).
They introduce a caveat by quoting Berger (1981, p. 49).
Note: Hattie's best quality study on Feedback, Kluger & DeNisi (1996) got an effect size = 0.38
3. Goldstein et al. (2000) state their aim:
Summary of results from page 401:
In Myth #17: Class size doesn't matter; reducing class sizes will not result in more learning, the 21 scholars collaboratively say,
"Fiscal conservatives contend, in the face of overwhelming evidence to the contrary, that students learn as well in large classes as in small... So for which students are large classes okay? Only the children of the poor?"2. McGiverin et al. (1989).
This study was only on 2nd-year students with properly controlled studies using experimental and control groups (although not randomly assigned). They decided a more pragmatic definition of a large class size is about 26 and a small class size is about 19 (p. 49).
So this study is specifically comparing a class size of about 26 students with 19 students.
So this is a totally different study than the Glass & Smith study above, which was looking at a range of different class size comparisons.
Barwe and Dahlström (2013) also point out the difference between this and the Glass & Smith study. Also, they point out Hattie claimed his focus was on reducing 25 students down to 15, which is different to reducing 26 students down to 19 (p. 19).
McGiverin et al., state that, the lack of experimental control and diverse definitions of large and small are among the reasons cited for inconsistent findings regarding class size (p. 49).
They introduce a caveat by quoting Berger (1981, p. 49).
"Focusing on class size alone is like trying to determine the optimal amount of butter in a recipe without knowing the nature of the other ingredients."Whilst they get a reasonably high d = 0.34 they advise caution in the interpretation of this result (p. 54). Also, they make special mention of the confounding variables - the Hawthorne effect, novelty, and self- fulfilling prophecy.
Note: Hattie's best quality study on Feedback, Kluger & DeNisi (1996) got an effect size = 0.38
3. Goldstein et al. (2000) state their aim:
"The present paper focuses more on the methodology of meta-analyses than on the substantive issues of class size per se."For a more detailed discussion on class size, they recommend looking at their previous papers (p. 400).
Summary of results from page 401:
Hattie reports but does not detail how he got 0.20 from the above table. It seems that Hattie just averaged all the DIFFERENT class size reductions (= 0.206).
Once again, this is at odds with Hattie's original claim that he focused on class size reductions of 25 down to 15 (VL, p. 87).
Also, a comparison of the studies shows different definitions for small and normal classes, e.g. study 2 defines 23 as a small class whereas in study 9 a normal class.
Nielsen & Klitmøller (2017) in Blind spots in Visible Learning - Critical comments on the "Hattie revolution", discuss the disparate definitions of large and small classes in different studies (p. 7).
So comparing the effect size from different studies is not comparing the same thing!
Goldstein et al., comment on another problem we have seen throughout VL (p. 403),
So once again, the detail of the study is lost when Hattie uses ONE averaged effect size (d) to represent that study.
Nielsen & Klitmøller (2017) in Blind spots in Visible Learning - Critical comments on the "Hattie revolution", discuss the disparate definitions of large and small classes in different studies (p. 7).
So comparing the effect size from different studies is not comparing the same thing!
Goldstein et al., comment on another problem we have seen throughout VL (p. 403),
"we have the additional problem that different achievement tests were used in each study and this will generally introduce further, unknown, variation."From a later paper, Goldstein et al. (2003), the 4 scholars contradict Hattie's claim that age makes no difference,
"Our results show how vital it is to take account of the age of the child when considering class size effects." (p. 20)They give more detail about the complexity of class size,
"A reduction in class size from 30 to 20 pupils resulted in an increase in attainment of approximately 0.35 standard deviations for the low attainers, 0.2 standard deviations for the middle attainers, and 0.15 standard deviations for the high attainers" (p. 17).
So once again, the detail of the study is lost when Hattie uses ONE averaged effect size (d) to represent that study.
These 3 Studies Confirm Teacher's Experience that Class Size Matters.
Steven Kolber's response to why Class Sizes do matter in Education, in response to John Hattie's article 'What doesn't work in Education: The Politics of distraction'.- here.
Most teachers would agree with Australian of the Year & teacher, Eddie Woo who said (video here - @ 41min):
Most teachers would agree with Australian of the Year & teacher, Eddie Woo who said (video here - @ 41min):
"Don't tell me that class size does not make a difference!"
The National Reading Panel (2000)
"Small-group instruction produced larger effect sizes on reading than individual instruction or classroom instruction..." (Ch2, p. 5)
More detail about class size here-







And my meta review of research also concludes that CSR had enormous impact on student outcomes in particular for children from disadvantage communities. See ANZSOG journal online Evidence Base
ReplyDeleteThanks David, your evidence about the the quality of teaching and learning as it relates to class size is very relevant. I've included some of your findings and insights into the commentary about class size. thank you
DeleteAll teachers should read this! Thank you.
ReplyDeleteI always thought Hattie was wrong on this, every teacher knows class size makes a difference.
ReplyDeleteAny actual teacher knows class size matters. I make a point of micro-teaching all of my students and have lists and records to ensure that this is equitable. It is very hard with 25 students in each of my secondary classes but I do it because the students know I know them and we can set individual goals. Less students equals more time to have an impact.
ReplyDeleteThanks, yes, agreed, every teacher knows class size matters. It's just that Administrators and Principles claim Hattie's overrides teacher experience. Few teachers know that Hattie is widely criticised in the peer reviews and that he misrepresents the actual studies. I'm trying to show that.
ReplyDeleteThank you George, what we need is a single repository of these peer reviews that challenge Hattie, so that teachers can access them in the battle against their administration. Thanks again. Sorry I have to comment anonymously, but its gotten that bad here!
ReplyDeleteGert Biesta wrote in 2010 warning Hattie's evidence base would become a form of totalitarianism. He was correct. So i understand the pressure on teachers not to question and conform. Please share this repository with your colleagues and if you are in a Union, express an opinion to them they need to challenge this. It is possible we can change this.
ReplyDeleteExcellent blog! Thank you!
ReplyDelete